
Beskrivelse
Du kender sikkert tre på stribe på et spillebræt med 3 · 3 felter (Kryds og Bolle). På sådan et spillebræt kan man finde 8 forskellige måder at få tre på stribe.
Hvad nu hvis vi spiller tre på stribe i 3D, altså på 3 · 3 · 3 felter – på hvor mange måder er der så at få tre på stribe?

Klassetrin
5.-9. klasse
Undersøgende arbejdsmåde der er fokus på i aktiviteten.
Samt beskrivelse af hvordan.
Når fokus er på at samle op og kommunikere resultater, betyder det, at eleverne skal foretage en løbende kommunikation undervejs i aktiviteten og ikke blot til sidst. Pointen ved dette er, at eleverne ved løbende kommunikation får et fælles sprog omkring, hvordan de ”ser” mulighederne for tre på stribe, hvordan de tæller op, altså hvilken systematik de anvender.
Det er ligeledes vigtigt, at eleverne undervejs noterer deres delresultater, så de ikke mister eller glemmer dem. Disse noter vil også hjælpe eleverne til at opdage, hvis deres systematik ikke er konsistent; at systematikken enten overser mulige vinderstriber eller tæller nogle dobbelt.
Andre elementer der er i fokus
fx andre undersøgende arbejdsmåder, matematiske kompetencer og stofområder.
Eleverne vil naturligt have brug for at ræsonnere og begrunde matematisk, når de skal overbevise sig selv og hinanden om, at deres fremgangsmåde vil give det rigtige resultat.
Sådan kan du starte din aktivitet op.
Forslag til iscenesættelse, som kan justeres i forhold til den enkelte klasse og skole.
Tag et klassisk Kryds og Bolle spil med ind i klassen og vis det til eleverne. Spørg om de kender spillet. Plejer de at vinde, når de spiller? Har de overvejet, på hvor mange måder de kan få tre på stribe? Find svaret sammen og diskuter, hvordan I fandt frem til svaret.
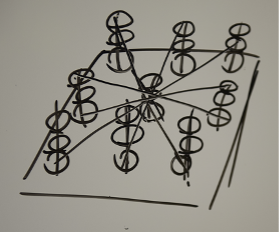
Tegn eller vis nu tre almindelige spilleplader over hinanden på tavlen som her:

Find sammen et eller to eksempler på vinderstriber – uden at etablere en særlig systematik eller sprogbrug, det skal eleverne selv etablere i deres eget arbejde med aktiviteten.
Nu stilles eleverne et af disse spørgsmål:
Hvad eleverne skal foretage sig.
Spørgsmål eleverne kan blive stillet undervejs og mulige udvidelser af aktiviteten.
Aktiviteten er oplagt at løse i små grupper, hvor eleverne både kan støtte og udfordre hinanden i arbejdet med at få systematiseret optællingen af vinderstriber.
Det kan være en ide at have ark med fortrykte 3D spilleplader, da det for nogle elever vil tage for meget fokus at få tegnet spillepladerne i hånden. Download elevark øverst på siden.
Hjælpespørgsmål til grupper, der har brug for det:
Spørgsmål, som udvider aktiviteten og som skaber yderligere undersøgelse:
Fire eksempler på systematikker (metoder):
Læs uddybning af systematikkerne her: https://nrich.maths.org/895
Det er ikke tanken, at eleverne skal have udleveret en metode, de skal ”gøre efter”, men hvis de ikke selv kan finde på andre systematikker, så kunne de præsenteres for den overordnede ide i en af de viste metoder og så selv udvikle systematikken derfra.
Prøv evt. at spille fire på stribe mod hinanden her: https://www.mathsisfun.com/games/foursight-3d-tic-tac-toe.html
Tip: Overvej, hvad der sker, når vinderstriberne i 3 · 3 · 3 kuben forlænges ud i 5 · 5 · 5 kuben.
(Da hver vinderstribe i 3 · 3 · 3 kuben peger unikt på netop to felter i det tilføjede lag, et felt i hver ende og alle felterne i det tilføjede lag bliver peget på, kan antallet af vinterstriber i kuben findes ved hjælp af formlen, som netop giver antallet af tilføjede felter delt med to.)
Hvordan kan aktiviteten afrundes og hvad er vigtigt at tale om samlet på klassen.
Når eleverne har udarbejdet et bud på antallet af vinderstriber, giver det rigtig god mening at få de enkelte grupper til at dele deres fremgangsmåde (systematik). Dette kan gøres på flere forskellige måder:
Forslag til spørgsmål fælles i klassen:
Eksempel på hvordan et svar kan tænkes og systematiseres.
Samt eksempel på elevarbejde med aktiviteten.
Der er nogle rigtig fine beskrivelser af fire forskellige systematikker til at finde antallet af vinderstriber her: https://nrich.maths.org/895
På disse billeder ses eksempler på gennemførelse af aktiviteten, mens den er i proces



Inspireret af
Aktiviteten er kendt flere steder fra. Hos nrich er der som nævnt gode eksempler på systematikker til sammentælling: https://nrich.maths.org/895